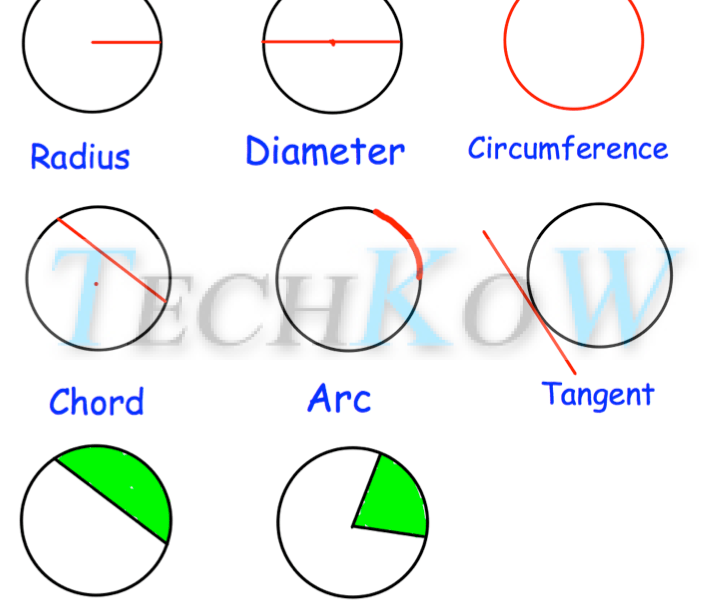
Η τυπική εξίσωση του κύκλου ορίζεται τέλεια ως X μείον H ολόκληρο τετράγωνο συν Υ μείον K ολόκληρο τετράγωνο είναι ίσο με την ακτίνα Τετράγωνο. Στη συγκεκριμένη εξίσωση, H και K θα είναι οι συντεταγμένες του κέντρου του κύκλου και το R θα είναι η ακτίνα του κύκλου. Πριν από την εξαγωγή αυτής της συγκεκριμένης εξίσωσης, είναι πολύ σημαντικό για τα παιδιά να είναι σαφείς σχετικά με τον βασικό ορισμό του κύκλου. Ο κύκλος θεωρείται ότι είναι ένα σύνολο από όλα τα σημεία που απέχουν ίσα από ένα σταθερό σημείο στο επίπεδο και το σταθερό σημείο θα είναι πάντα γνωστό ως το κέντρο του κύκλου. Η απόσταση μεταξύ του κέντρου και οποιουδήποτε σημείου της περιφέρειας θα αναφέρεται ως η ακτίνα του κύκλου.
Ο κύκλος είναι μια κλειστή καμπύλη που έχει σχεδιαστεί από ένα σταθερό σημείο γνωστό ως κέντρο στο οποίο όλα τα σημεία της καμπύλης θα έχουν την ίδια απόσταση από το κεντρικό σημείο. ο εξίσωση κύκλου έχει εξηγηθεί παραπάνω και περαιτέρω, τα παιδιά πρέπει να είναι ξεκάθαρα για κάθε στοιχείο της εξίσωσης, ώστε να μην αισθάνονται ποτέ σύγχυση τη στιγμή της εφαρμογής της στις ερωτήσεις. Η συνάρτηση έχει σχεδιαστεί τέλεια από κάθε τιμή στον τομέα που θα συσχετίζεται ακριβώς με ένα σημείο στον συντομέα και η γραμμή που θα διέρχεται από τον κύκλο θα αλληλεπιδρά με τη γραμμή σε δύο σημεία της επιφάνειας. Ως εκ τούτου, στον μαθηματικό τρόπο περιγραφής της εξίσωσης κύκλου μπορεί να παρασχεθεί σε διάφορα είδη μορφών όπως γενική μορφή, τυπική μορφή και διάφορες άλλες επιλογές.
- Εξίσωση του κύκλου όταν το κέντρο είναι η αρχή: Στο συγκεκριμένο σημείο η εξίσωση του κύκλου θα βγει X τετράγωνο συν το Y Το τετράγωνο είναι ίσο με το Α τετράγωνο.
Στην περίπτωση μιας εναλλακτικής μεθόδου αυτού του συγκεκριμένου σημείου, η εξίσωση θα είναι Χ τετράγωνο συν γιατί το τετράγωνο είναι ίσο με την ακτίνα Τετράγωνο.
- Εξίσωση κύκλου όταν το κέντρο δεν είναι αρχή: Στη συγκεκριμένη περίπτωση η εξίσωση έχει εξηγηθεί ως εξής: X μείον Β ολόκληρο τετράγωνο συν Υ μείον Κ ολόκληρο τετράγωνο ισούται με ένα τετράγωνο και αυτό αναφέρεται ως η τυπική μορφή για την εξίσωση ενός κύκλος.
Το να είμαστε σαφείς σχετικά με ορισμένους από τους τύπους που σχετίζονται με τον κύκλο είναι μια άλλη πολύ σημαντική πτυχή που πρέπει να αναλάβουν οι άνθρωποι, ώστε να μπορούν να λύσουν τις εξισώσεις τέλεια χωρίς κανένα είδος προβλήματος. Κάποια από τα οι τύποι εξηγούνται ως εξής:
- Η διάμετρος είναι ίση με τη διπλάσια ακτίνα
- Η περιφέρεια είναι ίση με 2 στην τιμή του pi στην ακτίνα
- Το εμβαδόν είναι ίσο με το pi στο τετράγωνο της ακτίνας
Το να είμαστε ξεκάθαροι σχετικά με την εφαρμογή όλων αυτών των τύπων στην εξίσωση ενός κύκλου είναι ένα άλλο πολύ σημαντικό πράγμα και εκτός από αυτό τα παιδιά πρέπει επίσης να είναι ξεκάθαρα για κάθε στοιχείο της φόρμουλας, ώστε να μπορούν να εφαρμόσουν τα πράγματα τέλεια. Επίσης, η σαφήνεια σχετικά με την εφαρμογή της τιμής του pi είναι μια άλλη πολύ σημαντική πτυχή που πρέπει να ξεκαθαριστεί στο μυαλό των μαθητών, ώστε να μην μπερδεύονται ποτέ στην εξέταση και να μπορούν να πάρουν καλούς βαθμούς χωρίς κανένα πρόβλημα. Επίσης, είναι πολύ σημαντικό για τα παιδιά να εγγραφούν σε πλατφόρμες όπως το cuemath.com όπου θα διδάσκονται από τους ειδικούς και κάθε πτυχή όπως η εξίσωση του κύκλου, η διάμετρος, η περιφέρεια, η χορδή, η εφαπτομένη και διάφορα άλλα είδη θα γίνει απόλυτα ξεκάθαρο στο μυαλό των παιδιών, έτσι ώστε να είναι ξεκάθαρα για τα πάντα και να είναι περαιτέρω πολύ επιτυχημένα όσον αφορά την εκπλήρωση των συνολικών σκοπών τους χωρίς καμία εξαιρετική ταλαιπωρία σε όλη τη διαδικασία.